For which pair of functions is composition possible? This question delves into the fascinating world of functions, where we explore the intricacies of function notation, inverse functions, composite functions, and their captivating interplay. Join us on an intellectual adventure as we uncover the secrets of function composition and its implications for the mathematical landscape.

In this exploration, we will unravel the concept of function notation, providing examples to illuminate its application. We will then venture into the realm of inverse functions, defining their characteristics and exploring the conditions that govern their existence. Our journey will continue with composite functions, where we will witness the process of combining functions and delve into the intricacies of simplifying these compositions.

Function Notation

Function notation is a concise way to represent the relationship between a function and its input. It involves using a letter, typically f, to represent the function, followed by parentheses containing the input variable. The output of the function is then written as f( x), where xis the input variable.

For example, if we have a function that squares its input, we can represent it using the notation f( x) = x². This means that when we input a value for x, the function will output the square of that value.

Domain and Range

The domain of a function is the set of all possible input values, while the range is the set of all possible output values. For the function f( x) = x², the domain is all real numbers, since we can input any real number and the function will output a real number.

The range, however, is only non-negative real numbers, since the square of any real number is always non-negative.

Inverse Functions

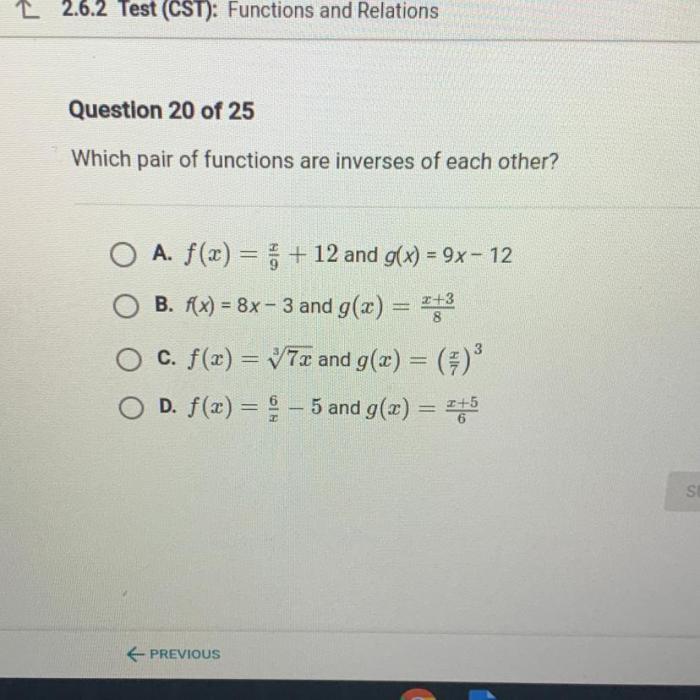
Inverse functions are functions that “undo” each other. In other words, if you apply one function to a number and then apply its inverse to the result, you get back the original number.

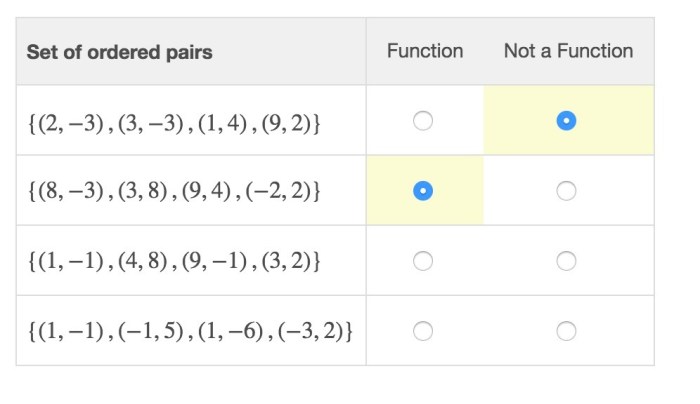
For a function to have an inverse, it must be one-to-one, which means that each input value corresponds to exactly one output value.

Examples of Functions with Inverses, For which pair of functions is

• The function f(x) = x^2has an inverse because it is one-to-one. The inverse function is f^-1(x) = sqrt(x).
• The function g(x) = sin(x)does not have an inverse because it is not one-to-one. For example, g(0) = g(π) = 0, so there is no unique inverse function that would map 0 back to both 0 and π.

Composite Functions

In mathematics, a composite function is a function that is formed by applying one function to the output of another function. The process of combining functions in this way is called function composition.

So, let’s see. For which pair of functions is… I’m not sure if you know about unit 5 mcq ap human geography , but it might help. Anyway, back to our question, for which pair of functions is…

Composing Functions

To compose two functions, f( x) and g( x), we first evaluate f( x) and then substitute the result into g( x). The resulting function, denoted as g( f( x)), is the composite function.

In other words, g( f( x)) = g( y), where y= f( x).

Examples of Composite Functions

Let’s consider the following functions:

• f( x) = x+ 2
• g( x) = x²

To compose g( f( x)), we first evaluate f( x) and then substitute the result into g( x):

“`g(f(x)) = g(x + 2) = (x + 2) <sup>2</sup>= x <sup>2</sup>+ 4x + 4“`

Therefore, the composite function g( f( x)) is x²+ 4 x+ 4.

Function Composition and Inverse Functions: For Which Pair Of Functions Is

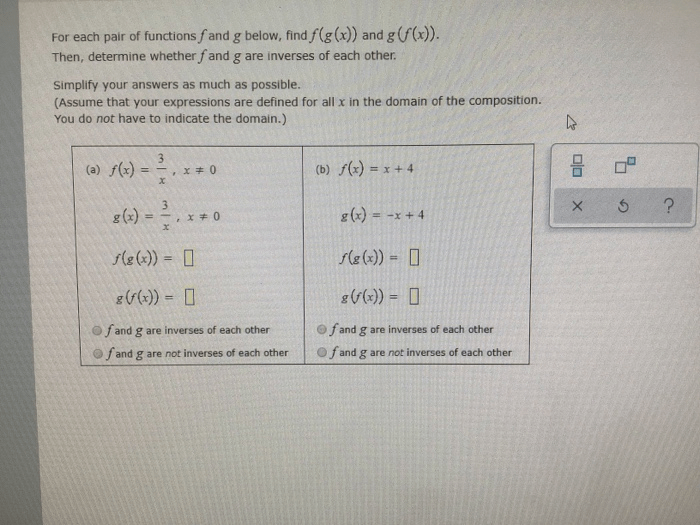
Function composition and inverse functions are two important concepts in mathematics that are closely related. Function composition is the process of combining two functions to create a new function, while an inverse function is a function that undoes the operation of another function.

To find the inverse of a composite function, we need to first find the inverse of each individual function in the composition. Once we have the inverses of each function, we can then compose them in the opposite order to get the inverse of the composite function.

Example

For example, let’s say we have the following composite function:

$$f(x) = (x + 2)^3$$

To find the inverse of this function, we first need to find the inverse of the function $(x + 2)$. The inverse of this function is $x – 2$. We then need to find the inverse of the function $x^3$.

The inverse of this function is $x^1/3$. Composing these two inverse functions in the opposite order, we get the inverse of the composite function:

$$f^-1(x) = (x^1/3

2)$$

Graphical Representation of Functions

Graphing functions is a fundamental skill in mathematics. It allows us to visualize the relationship between the input and output of a function and to understand its behavior.

Functions are graphed on a Cartesian coordinate system, which consists of two perpendicular axes: the x-axis (horizontal) and the y-axis (vertical). The point where the axes intersect is called the origin.

Types of Graphs

There are various types of graphs that can be used to represent functions. The most common types include:

• Line graphs: Represent linear functions, which have a constant rate of change.
• Parabola graphs: Represent quadratic functions, which have a U-shaped or inverted U-shaped graph.
• Circle graphs: Represent functions that involve trigonometric functions.
• Exponential graphs: Represent functions that involve exponential growth or decay.

Graphing Functions

To graph a function, we need to plot the points that satisfy the equation of the function. We can do this by assigning different values to the input variable (x) and calculating the corresponding output value (y) using the equation of the function.

Once we have plotted a sufficient number of points, we can connect them with a smooth curve to obtain the graph of the function.

Interpreting Graphs

Graphs of functions can provide valuable information about the behavior of the function. We can use graphs to:

• Determine the domain and range of the function.
• Find the intercepts of the function (where it crosses the x-axis and y-axis).
• Identify the maximum and minimum values of the function.
• Determine the slope of the function (for linear functions).

Transformations of Functions

Function transformations are a way to manipulate functions by shifting, flipping, or stretching their graphs. This allows us to create new functions with different properties from the original function.

There are three main types of function transformations:

Translations

Translations move the graph of a function horizontally or vertically without changing its shape. A horizontal translation moves the graph left or right, while a vertical translation moves the graph up or down.

• Horizontal translation: f(x) → f(x + a)(moves the graph aunits to the left if ais positive, or aunits to the right if ais negative)
• Vertical translation: f(x) → f(x) + b(moves the graph bunits up if bis positive, or bunits down if bis negative)

Reflections

Reflections flip the graph of a function over the x-axis or the y-axis. A reflection over the x-axis changes the sign of the y-coordinates, while a reflection over the y-axis changes the sign of the x-coordinates.

• Reflection over the x-axis: f(x) →-f(x)
• Reflection over the y-axis: f(x) → f(-x)

Stretches

Stretches change the slope or the width of the graph of a function. A vertical stretch changes the slope of the graph, while a horizontal stretch changes the width of the graph.

• Vertical stretch: f(x) → af(x)(stretches the graph vertically by a factor of aif ais positive, or shrinks the graph vertically by a factor of aif ais negative)
• Horizontal stretch: f(x) → f(bx)(stretches the graph horizontally by a factor of bif bis positive, or shrinks the graph horizontally by a factor of bif bis negative)

Function transformations are a powerful tool for manipulating functions and creating new functions with different properties. By understanding the different types of transformations, you can easily transform any function to meet your specific needs.

Helpful Answers

What is the relationship between function composition and inverse functions?

Function composition and inverse functions are closely related. The composition of two functions can result in an inverse function, and vice versa. This relationship provides a powerful tool for analyzing and manipulating functions.

How do you determine if a function has an inverse?

To determine if a function has an inverse, we need to check whether it is one-to-one. A function is one-to-one if each element in the domain maps to a unique element in the range. If a function is one-to-one, it has an inverse.

What are the applications of function composition in real-world scenarios?

Function composition has numerous applications in various fields. For instance, in physics, it is used to model the composition of forces acting on an object. In computer science, it is employed to create complex algorithms by combining simpler ones.